黔江区人民中学 张成林
杠杆在力的作用下处于静止或匀速转动我们就说杠杆平衡了;杠杆可以平衡在任意位置。我们将杠杆平衡在水平位置只是一种特殊情况,主要是为了量取力臂方便(如果杠杆平衡在水平位置, 阻力,动力分别是悬挂在杠杆上的钩码的重力,方向竖直向下,动力臂, 阻力臂分别是动力,阻力作用点到支点竖直延长上杠杆的长度)。
物理实验室使用的天平是等臂杠杆,既然是杠杆就应该能平衡在任意位置。但事实上天平只能平衡在水平位置,即如果天平已经平衡在水平位置,外力强迫使之平衡在其它位置,外力撤去后,天平又会自动回到水平位置,这又是为什么呢?
天平结构中,横梁,托盘,游码,标尺,指针,平衡螺母等效于一个杠杆(以下简称等效杠杆,重力设为G0 ,左托盘里所放物体的重力设为G1,砝码的重力设为G2),等效杠杆的重心位置D(图中用小黑点表示)与支点O(图中用黑三角形表示,是等效杠杆在水平方向的中点)的位置关系将决定杠杆在哪些位置可以保持平衡。调节平衡螺母,就是要调节重心D和支点O重合或在同一竖直线上。
一、 当把支点O与重心D重合。
1. 等效杠杆在水平位置平衡时如图1有G1×AO=G2×BO。G0的作用线过支点,力臂为0对杠杆的转动没有贡献。
2. 当杠杆顺时针旋转 角后如图2:
AO•cos =EO BO•cos =OH 所以 G1•EO=G2•OH,杠杆仍处于平衡状态。
杠杆转到任意位置杠杆都是平衡的,这种杠杆的平衡就是随遇平衡。
如果天平采用这种构造结构,使用起来很不方便。本来梁横梁已经在水平位置平衡的天平,会在扰力作用下,离开水平位置,而静止在其它位置,我们将误认为天平原来没有平衡。
二、 当把支点O选在重心D的竖直下方。
1. 等效杠杆在水平位置平衡时如图3,根据杠杆平衡条件有:
G1×OC=G2×OK。很容易得
G1×AD=G2×BD
G0的作用线过支点,力臂为0对杠杆的转动没有贡献。
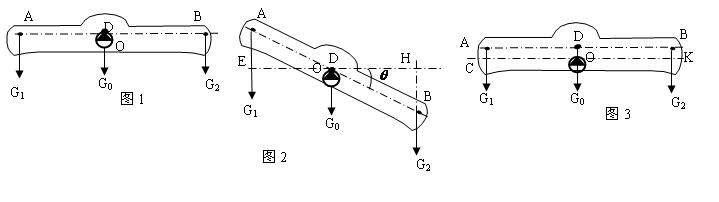
2.当杠杆顺时针旋转 角后如图4:
AD•cos =ED > O C′ , BD•cos =DH
G1•O C′
如果天平采用这种构造成结构,使用起来非常不方便:一是在添加较小的砝码时,必须把天平横梁左右各偏转一次才能确定砝码是偏大了还是偏小了。二是砝码添加得恰到好时,即物体的质量等于砝码的质量时,由于受到微小扰力作用,天平的横梁将失去原来的平衡后不能自动恢复在水平位置平衡,使我们误认为是砝码没有添加准确。
三、 当把支点O选在重心D的竖直上方.。
1. 等效杠杆在水平位置平衡时如图5,根据杠杆平衡条件有:G1×OC=G2×OK。很容易出G1×AD=G2×BD。G0的作用线过支点,力臂为0对杠杆的转动没有贡献。
2. 当杠杆顺时针旋转 角后如图6:
AD•cos =ED < O C′ ,
BD•cos =DH>OK′ ,
G0的力臂是MO,所以很明显有
G1•O C′+ G0•MO >G2•OK′,杠杆不平衡。其左端将要下降,当到达水平位置时有G1×AD=G2×BD,但由于惯性,其右端还会升高,而后又会下降……。这样来回几次后,等效杠杆又会平衡在水平位置。
如果天平采用这种构造成结构,调节在水平位置天平,在受到微小扰力偏离平衡状态后,会自动恢复原来的平衡状态,这种平衡就是稳定平衡。
物理实验室的天平就是采取这种结构制造的,因此横梁只能在水平位置平衡。
如果天平中没有放物体和砝码,只是调节天平横梁的情形,即可令上述讨论中的G1 G1为0,结果是一样的。
 您的位置:>>
您的位置:>> 