【高中组一等奖】宇宙空间站中模拟重力的探索及“洛书”思想的应用猜想　　

重庆八中 高2017级11班  贺思齐　　

如今人类对太空探索的竞争越来越激烈，但只有极少数国家已经建成了自己的宇宙空间站，中国也在这方面步步紧追。可是，在太空中没有重力，给宇航员的生活带来了诸多不便。东西四处乱飘，很容易找不到，而且细小的物质还可能通过机器的缝隙钻进机器造成破坏，这对宇航员的生命威胁是有很大影响的。那么，在空间站中制造人工重力的做法就势在必行了。　　

根据牛顿第三定律和向心力的原理，我们可以做如下探究：　　

1、空间站是圆形的    　　

当空间站以圆形来建造时，我们可以在圆形建造一个转动装置，当空间站转动起来时在内壁上的人会由于向心力的作用产生类似受到重力的效果。

由此可得出：一个半径为100m　的空间站的角速度为0.313 rad/s，线速度为　31.3m/s时，即可在内壁上产生9.8m　/s²的向心加速度，又根据牛顿第三定律，与内壁接触的人便会受到类似重力的一个始终垂直于空间站内壁的向外的力的作用，由此受到类似重力的效果　　

同时，我们可以对这个数据再次详细计算一下：　　

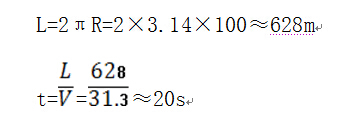
    得出：一个半径　100m　的空间站内在产生人工重力后的旋转速度使它20s内必须转一圈，也就是说它的角速度必须为0.313 rad/s，外壁线速度必须达到　112.68km/h　，这看上去似乎有点快　　

    于是，我们便可以制作这样一个函数图像来判断空间站旋转角速度随半径增加的趋势：　　

其中X轴为空间站半径，单位m；Y轴为空间站旋转角速度，单位为rad/s。函数左端点X轴取值为1，右端点X轴取值为600,中间每个数据差值为1　　

根据此图我们可近似得出，当空间站半径越大时，要提供　9.8m　/s²的向心加速度的所需角速度随速度变化越不明显。且在数据40至50的前后趋势变化很大。前面变化落差巨大，而后面落差极小。　　

更多的，我们还可以画出使空间站重力效果为　0.8g　、　0.6g　、　0.5g　时的图像：　　

对比后发现，g取值不同时变化趋势事实上并无大异　　

同时，我们可看出要在半径和角速度间找一个最佳平衡点，即取值点左右两边的函数图像变化趋势差距最小，这个平衡点应在这个范围之内：　　

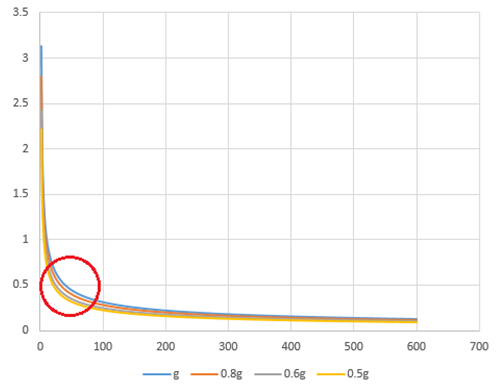
但由于在函数中在横坐标和纵坐标之间寻找一个“最佳平衡点”并不简单，这需要顾及到横坐标和纵坐标之间都达到一个“最佳状态”，而代数中没有这样的公式来计算。这也可能是目前这种装置的思想并没有应用到太空中的重要原因之一。　　

但是，我们可以利用中国古代“洛书”的思想。　　

“洛书”原本是刻在龟甲上的一些黑白点，现代人将其图像化并扩展，便得到了一个四阶的数列方阵：　　

    我们观察以上方阵，分别有4个纵列和横列，而这4个纵列和横列中存在一个神奇的等量关系：　　

首先，我们将纵列的每一列的4个数字相加：①8+13+3+10=34　　

                                        ②11+2+16+5=34　　

                                        ③ 14+7+9+4=34　　

                                        ④1+12+6+15=34　　

很明显，4组数字相加均为定和34，而这16个数字分别是1到16的整数　　

同样的，将横列的4组数字每组相加，得到的和仍然是34　　

    更巧妙的是，沿着这个方阵的两条对角线上的数字相加：　　

①1+7+16+10=34　　

② 8+2+9+15=34　　

定和仍然是34  　　

    这就是这个方阵的奇妙之处。若要用西方代数来得出这个方阵，是绝对不可能的，但中国古代就已经将其解出来了。假如这是一个军事上的布阵，那么无论敌人从什么方向进攻，此阵的防御力都是相同的，都为34，这便是一种“最佳状态”。　　

    同时，我们还有将任何普通数字方阵变为“洛书”方阵的方法，这大大加强了灵活性，更况且“洛书”里的数字都没有重复的。　　

因此，我们可以提出这样的假设：将“洛书”与数学函数结合起来，找到一个可联系两者的桥梁，这样就能将以上空间站半径和角速度之间的“最佳状态”解出来。　　

    当然以本人浅陋的学识，尚无法在有限的时间内将这个假设付诸于行动。但只要在这两者之上用心探索，就一定能使人类在太空中也能像在地球上的梦想成为现实。

想法十分有趣，并且运用到自己所学的物理知识，整片文章的条理比较清晰，并且引用了其他知识，知识面广，希望继续去发现、探索！　　

                                       指导教师:翟建平